【宇宙機】熱設計ってなにしてるの？

※本記事は、東京大学航空宇宙工学科／専攻 Advent Calendar 2018 11日目の記事です。

はじめに

アドベントカレンダーに寄稿するにあたって、自分がまともに書けそうな内容は宇宙機熱設計の話くらいかなと思い、この内容としました。といっても、まだ経験も浅いので「ここは違うだろ！」みたいなところもあるかもしれません。

前日の10日目の記事は宇宙機構造について、明日の12日目の記事は宇宙機の制約条件下でのプログラミングについてで、怒涛の3日連続宇宙機設計の流れとなっております。

本記事では、そもそも熱設計が何かということから、EQUULEUS*1の例*2も挙げながら熱設計の実装の話、そしておまけとして航空宇宙工学科にまとわりつく卒業設計の熱設計の話までを取り上げます。色々書いてたら長くなったので、適宜目次を使って読みたいところだけ読んでください。

はじめに
熱設計ってなに？なんで必要なの？
熱の伝わり方とそのモデル化
- 伝導
- 放射
熱平衡方程式
熱設計の方針の立て方
- 衛星か探査機かによる熱設計の違い
- 熱設計の考え方及び実装
熱系の仕事
参考文献

熱設計ってなに？なんで必要なの？

結論から述べると、宇宙機における熱設計の目的は

「いついかなる時も、すべての搭載機器（コンポーネント）が、それぞれの動作可能な許容温度範囲内に収まるようにする」

ことです。

全ての電子機器には動作可能な温度範囲があり、これを逸脱するとパフォーマンスが下がり、最悪の場合故障してしまいます。

以下の表は、宇宙機に搭載される電子機器の許容温度範囲の例です。

コンポ	低温側	高温側
バッテリー	0	30
通信機器	-10	60
姿勢制御（SS、STTなど）	-20	60
PCU	0	60
光学カメラ	-10	40

電子機器の動作可能温度範囲を一番身近に感じられるのは、スマートフォンのバッテリーでしょうか。

皆さんは非常に暑い日や寒い日に外で歩きスマホをしていたら、突然バッテリーの消耗が激しくなり電源が落ちた、という経験はないでしょうか。これはスマートフォンに搭載されているリチウムイオン電池の動作温度範囲が大体0℃～30℃であり、これを逸脱する外気温下でスマートフォンを操作していたことによります。つまり、異常気象下では歩きスマホはしてはいけない、ということです（歩きスマホは常時してはいけません）。

このような少ない例を除き、地上にいる私たちは日ごろこのような動作温度範囲を気にすることはあまりありません。それでは何故宇宙では特別動作温度範囲を気にかけなければならないのでしょうか。

それは、宇宙の熱環境が地上と比較して圧倒的に厳しいからです。太陽-地球間の距離（1AU）では、大体1366W/m^2の熱量が太陽から降り注ぐ一方で、宇宙空間は3K（-270℃）という極低温環境にあります。よって太陽光が当たるか当たらないか、どの面に当たっているかによって、宇宙機の熱環境は大きく変動してしまいます。しかし、いかなる環境下でも宇宙機の全ての機器が正しく動いていなければ宇宙機全体としての機能は失われてしまうため、熱設計は宇宙機を開発するにあたってとても重要です。

それでは、この熱設計をするにあたって、熱がどのように流れるかについて復習していきましょう。

熱の伝わり方とそのモデル化

さて、熱設計を正しく行うためには熱の流れ方をコントロールする必要があり、そのためにはまず熱の伝わり方について知っていなければなりません。恐らく皆さん中高時代に習っているかと思いますが、熱の伝わり方には以下の3つがあります。

伝導：物質を通して熱が伝わる
対流：流体の移動によって熱が伝わる
放射：電磁波によって熱が伝わる

ここで真空環境下では対流を考えなくて良いので、伝導と放射のみをモデル化すれば良いことになります。この際の方針として、温度を考えたい物体を節点で代表させ、その節点間の熱のやり取りを考えます。その物体の温度全体を均一と扱って良いならば1つの節点で代表させることができますし、物体内での温度勾配もある程度表現したいならば複数節点に分割して考えることも可能です。このような節点法をベースに、伝導と放射のモデル（熱数学モデル）を考えます。

伝導

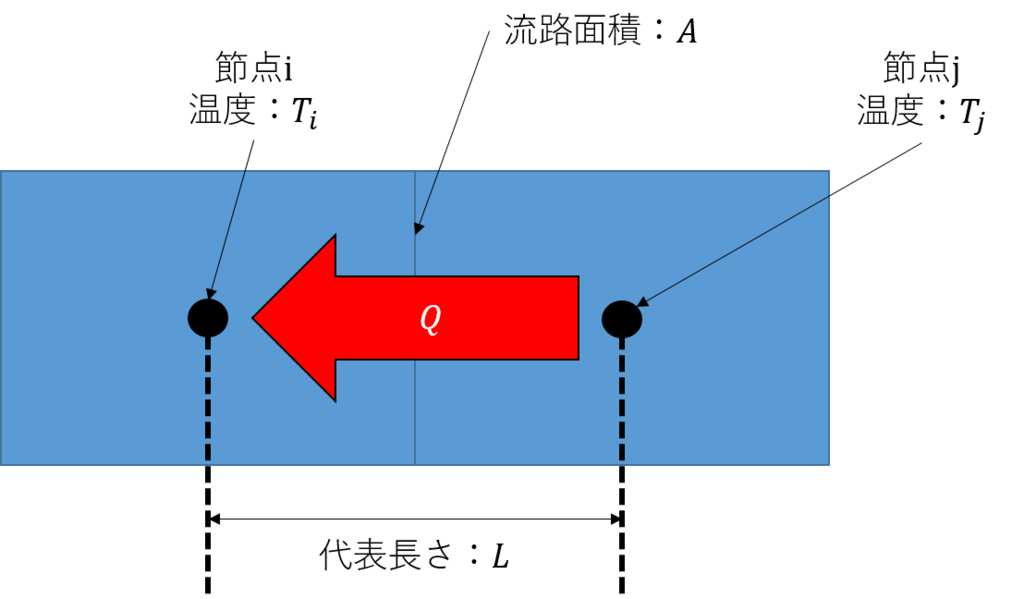
図のような2つの節点間の伝導による熱の移動量は、フーリエの法則によって両者の温度差に比例します。よって以下の式でモデル化ができます。

$Q_{cond} = C_{ij}(T_j - T_i) \tag{1}$

ここで、 $C_{ij}$ のことを2点間の熱コンダクタンスと呼び、単位は $[\rm{W/K}$ ]となります。

熱コンダクタンスは熱の流路の断面積 $A$ 及び2点間の代表長さ $L$ を用いて、以下のように概算できます。

$C_{ij}=kA/L \tag{2}$

ただし、 $k$ は熱伝導率 $[\rm{W/mK}$ ]であり、物質ごとに決められています。

また、異なる2つの物質の間の熱コンダクタンスを考える際には、各物体内での熱コンダクタンスを考えた後、それらを結合します。

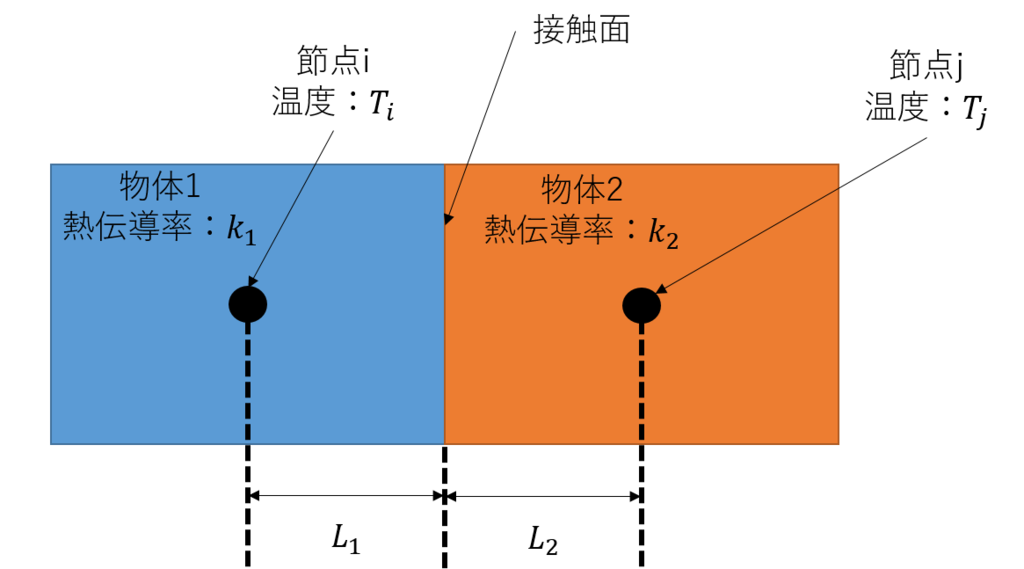
物体1内で、節点 $i$ から接触面の間の熱コンダクタンス $C_1$ は以下のように計算できます。

$C_1=k_1A/L_1 \tag{3}$

同様に物体 $j$ 内での熱コンダクタンス $C_2$ は以下のようになります。

$C_2=k_2A/L_2 \tag{4}$

これらを使って、節点 $i$ と節点 $j$ の間の熱コンダクタンス $C_{ij}$ は以下のように計算できます。

$\frac{1}{C_{ij}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_{contact}} \tag{5}$

ここで $C_{contact}$ を接触熱コンダクタンスといい、接触面の熱伝導のしやすさを表します。

ボルトで2つの面を締結している場合、 $C_{contact}=N \times 0.07$ と概算できます。ただし、 $N$ は接触面におけるボルトの本数です。

放射

放射によって2つの面の間で移動する熱量は、以下の式のように温度の4乗で効いてきます。

$Q_{rad} = R_{ij}(T_j^4 - T_i^4) \tag{6}$

ここで、 $R_{ij}$ を放射係数と呼び、以下の式で計算できます。

$R_{12}=\epsilon_1 \epsilon_2 F_{12} A_1 \tag{7}$

ただし、 $\epsilon_i$ は面 $i$ の放射率、 $F_{ij}$ は面 $i$ から面 $j$ を見た時の放射形態係数です。放射形態係数とはすなわち、面 $i$ が面 $j$ をどれほど「見て」いるかを表しています。イメージとしては以下の図で、面 $i$ の全視野のうち面 $j$ を見ている部分の割合のことを指します。

形態係数は以下の式で定義されますが、特殊な場合を除いて解析的に解くことはできません。

$\hspace{-20pt} F_{ij} = \frac{1}{\pi A_i} \int_{A_i} \int_{A_j} cos \theta_i cos \theta_j dA_i dA_j / r^2 \tag{8}$

この特殊な場合の例としては、以下の2つが挙げられます。スマホで式が見切れていたらごめんなさい。

①正対する2つの平面

$F_{ij}(\pi xy/2) = ln \{ (1+x^2) (1+y^2)/(1+x^2+y^2) \} ^{1/2} + y \sqrt{(1+x^2)}tan^{-1} \{y/\sqrt{(1+x^2)} \} \\ \hspace{60pt} + x \sqrt{(1+y^2)}tan^{-1} \{x/\sqrt{(1+y^2)} \} - y tan^{-1}y - x tan^{-1} x \tag{9}$

②直交する2つの平面

$\hspace{-20pt} F_{ij}(4\pi y) = ln \{ (1+x^2) (1+y^2)/(1+x^2+y^2) \} + x^2 ln \{ x^2 (1 + x^2 + y^2) / \{ (1+ x^2) (x^2 + y^2) \} \\ \hspace{40pt} + y^2 ln \{ y^2 (1 + x^2 + y^2) / \{ (1+ y^2) (x^2 + y^2) \} +4x tan^{-1}(1/x) + 4y tan^{-1} (1/y) \\ \hspace{-40pt} - 4 \sqrt{(x^2+y^2)}tan^{-1}\{1/\sqrt{(x^2+y^2)} \} \tag{10}$

マジでめちゃくちゃな式ですね。

また、形態係数に関して以下の式が成立します。

$A_i F_{ij} = A_j F_{ji} \tag{11}$

$\sum^n_{j=1} F_{ij} = 1 \tag{12}$

言葉にいいかえれば、立場を入れ替えてもお互いを見ている面積は一緒であるということと、ある面に関する形態係数を全て足せばその面の全視野をカバーしている、ということです。

式(9)～(12)を用いることで、直方体形状の宇宙機であれば大抵の形態係数を計算することができます。計算できなかったところはおおよそで頑張りましょう。

熱平衡方程式

ここまで書いてきた伝導及び放射に関するモデルを1つの式にまとめると、以下の熱平衡方程式になります。

$c_i \frac{dT_i}{dt} = Q_i + \sum^n_{j=1} C_{ij}(T_j - T_i) + \sum^n_{j=1} R_{ij}(T_j^4 - T_i^4) \tag{13}$

この式は簡単に要約すると、

（節点の温度上昇に使われる熱）＝（節点に入ってくる熱量）－（節点から出ていく熱量）

となります。

ここで $c_i$ は比熱、 $Q_i$ は伝導と放射以外の熱入力で、代表的なものは以下に挙げられます。

節点上のコンポーネントの発熱
太陽からの放射入熱

太陽からの放射入熱は以下の式で表されます。

$Q_{si} = \alpha_i A_i E_s$

$E_s$ は太陽定数で、1AUでは冒頭に述べた通り $E_s = 1366[\rm{W/m^2}$ ]で、太陽からの距離の2乗に反比例します。遠日点での火星は2.43AUなので、 $E_s = 231[\rm{W/m^2}$ ]と地球近傍での6分の1となります。

$\alpha$ は太陽光の吸収率*4で、 $\epsilon$ 同様物質ごとに決まっています。

他にも地球周回衛星の場合では地球赤外放射やアルベドを考えなければなりませんが、今回は省略します。

ここまで説明してきた熱平衡方程式を全ての節点に関して解くことで、各接点の温度を計算することができます。この計算結果が全ての節点に関して常時動作許容範囲内に収まるようにすることが熱設計の目的になります。

熱設計の方針の立て方

衛星か探査機かによる熱設計の違い

さて、ここまで熱設計のベースとなる熱平衡方程式について長々と書いてきましたが、ここからは本題となる、実際にどのようにして熱設計を行うかについてです。
まず、最初に重要なのはどのような軌道を飛ぶかです。地球周回衛星と深宇宙探査機では当然熱環境も大きく変わってきます。それぞれの熱設計の特徴は以下の通りです。

地球周回衛星：太陽定数は一定だが、太陽の方向が時々刻々変わっていくため、全ての面が太陽に晒される可能性がある。また、各接点の比熱を考えたうえで軌道数周分の非定常解析をする必要がある。
深宇宙探査機：（3軸姿勢制御であれば）常に太陽方向を一定にすることができるため、太陽があたる面とあたらない面を指定することができる。また、高温最悪条件と低温最悪条件の平衡状態（ $\frac{dT}{dt}=0$ ）についての定常解析を考えれば良い。

地球周回衛星では温度が1周期の間でおおよそ平均化されるため、無茶な熱設計になることはあまりないです。しかし、非定常な解析を考えなければならないので比熱の計算やルンゲクッタ等での実装が必要で、面倒です。

深宇宙探査機はミッションによっては相当厳しい熱設計になりえますが、定常な平衡状態のみを考えれば良いということで解析にかかるコストは低いです。

僕が今まで行ってきた熱設計は全て深宇宙探査機に関してなので、今回主に取り上げるはこちらになります。

熱設計の考え方及び実装

搭載コンポーネント・構造・軌道などが確定した状態で熱設計で変更することのできるパラメータは主に $C_{ij}$ 、 $\epsilon$ 、 $\alpha$ の3つです。それぞれに関してみていきます。

$Q_{cond} = C_{ij}(T_j - T_i) \tag{1}$

先ほども出てきたこの(1)式を見ると、節点 $i$ への入熱量を固定した場合、 $C_{ij}$ と $(T_j - T_i)$ は反比例します。すなわち、2節点間の温度差を大きくつけたい場合は $C_{ij}$ を小さく、逆に温度差を小さくしたい場合は $C_{ij}$ を大きくします。

具体的にEQUULEUSで行われている設計例としては、大きな熱量が必要な気化室と、大きな発熱のある通信系を大きな $C_{ij}$ で結合しています。

$\frac{1}{C_{ij}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_{contact}} \tag{5}$

式(5)を見てみると、 $C_1$ 及び $C_2$ は構造が確定している場合変更できないため、 $C_{contact}$ を変更することによって $C_{ij}$ を調整します。この変更の実装は、該当箇所に熱伝導性の良い素材（EQUULEUSではサーマルフィラー *5と呼んでいます）を挟んだりすることで行います。

一方で、表面特性と呼ばれる $\epsilon$ と $\alpha$ についてですが、これらが特に重要になるのは宇宙機の一番外側の構体パネルです。厳しい宇宙環境に直接晒される構体パネルの表面特性設計は、宇宙機熱設計の第一歩と言っても良いでしょう。

この時に活躍するのが、よく宇宙機の外面に貼ってある金ぴかの膜みたいなやつです。これはMLI (Multi Layer Insulation)と呼ばれる断熱材で、 $\epsilon$ と $\alpha$ がともに0に近いため、宇宙の熱環境から宇宙機内部を守るシールドの役割をしています。

ここで陥りやすい発想が、「とりあえず全部MLIで覆えば外の宇宙環境とか関係ないやん」というものです。これをしてしまうと宇宙機内部の発熱が外に逃げられなくなってしまうため、宇宙機の温度がひたすら上がり続けてしまいます。

これを防ぐために、一部の箇所は放熱面としてMLIで覆わずにしておきます。放熱面は $\epsilon$ を大きくしたいので基本的には黒色にするのですが、注意しなければならない点があります。それは黒色にすると $\alpha$ も大きくなるため、太陽光が当たると放熱と真逆の効果を発揮します。放熱面には絶対太陽を当てないような運用を考えましょう。EQUULEUSの場合は太陽光が入射することのない側面が放熱面として黒色になっています。

また、黒色以外の絶妙な表面特性値を使用したい場合は、アルミ材質や銀材質なども使用することができます。これらを実装するのに使うのが、熱制御テープと呼ばれているものです。EQUULEUSにおいては黒色面ではBlack Kapton、他の面ではAluminized KaptonやAg Teflonといったテープが使用されています。

テープ	α	ε
Aluminized Kapton	0.14	0.036
Ag Teflon	0.099	0.756
Black Kapton	0.874	0.811

更に奥の手として、どうしても低温側が逸脱してしまう節点に関してはヒーターを搭載し、適当な熱入力をその節点に加えるという手法も取れます。この際の注意として、高温側の逸脱に対しては処理できないことと、ヒーター出力の分だけ宇宙機全体の電力消費が増えるため、電力収支が厳しい場合は使えないということです。

これらのパラメータをイタレーションして、良い解を見つけることが熱設計の概要になります。

熱系の仕事

ここでは、熱設計を行う以外の熱系の仕事を紹介します。

Thermal Desktop解析

ここまで述べてきた熱解析モデルをCADベースで作成し、高速で計算することのできるThermal Desktopと呼ばれるアプリケーション上でモデルを作成し、解析を回します。

CADモデルのおかげで放射形態係数を計算する必要がないためとても楽ですが、インターフェースがかなり使いづらいのと環境構築が死ぬほど面倒くさい。

熱設計結果の実装

先ほど述べたMLIやヒーターの管理をしたり、サーマルフィラーを作成し該当箇所に貼り付けたり、構体パネルの外側に熱制御テープを貼り付けたりします。これも本当に面倒くさいですが、自分が貼ったテープがそのまま宇宙に飛ぶと考えるとワクワクします。またこれ以外にも、宇宙機の温度環境を知るための温度計などの管理・貼り付けも行います。

熱真空試験

ここまでの熱設計はあくまでモデルベースなので、実機でその熱設計が想定通り反映されているかどうかを確認しなければなりません。このために、真空チャンバの中に宇宙機を入れ、チャンバに液体窒素を流して極低温環境を模擬した熱真空試験を行う必要があります。この熱真空試験の計画・実施が熱系一番の大仕事であると言えます。同時に、宇宙環境を模擬した状況で宇宙機が健康に動くかどうかの電気試験も行います。